Logic came from the Greek word logos, means “discourse”, “reason”.
- It is defined as the study of the principles of correct reasoning.
A proposition is a declarative sentence which is either true or false but not both. A sentence which is both true and false is called a paradox. Paradox is not a statement.
Example:
- 2+2=5 (false), It is a proposition.
- kathmandu is the capital city of Nepal. (True), It is a proposition.
- Open the door. It is not a proposition.
Note: x>15, go there, who are you?
The above mentioned sentences are not propositions since we cannot say whether they are true or false.
Meaning of Propositional Logic:
Propositional Logic (PL), also known as sentential logic or Boolean logic, is a formal system used to represent and reason about statements that can be either true or false.
- It is a fundamental part of artificial intelligence, automated reasoning, and computer science.
1.) Syntax of Propositional Logic:
Syntax defines the rules for constructing valid expressions in propositional logic. A well-formed formula (WFF) in PL is built using the following components:
- Propositions (Atomic Sentences): These are simple statements that are either true or false, represented by symbols like P, Q, R (e.g., “It is raining” can be represented as P).
- Logical Connectives: These are operators used to combine propositions and form more complex statements:

A valid well-formed formula (WFF) follows the syntactical rules of propositional logic.
2.) Semantics of Propositional Logic:
Semantics defines the meaning of logical expressions. It determines how truth values are assigned to expressions based on the truth values of their components.
- The meaning of a complex proposition is determined by the truth values of its simpler components and how they are combined using logical connectives.
- Truth tables are used to evaluate the truth value of compound statements for all possible truth values of their atomic propositions.
Truth Tables for Logical Connectives:
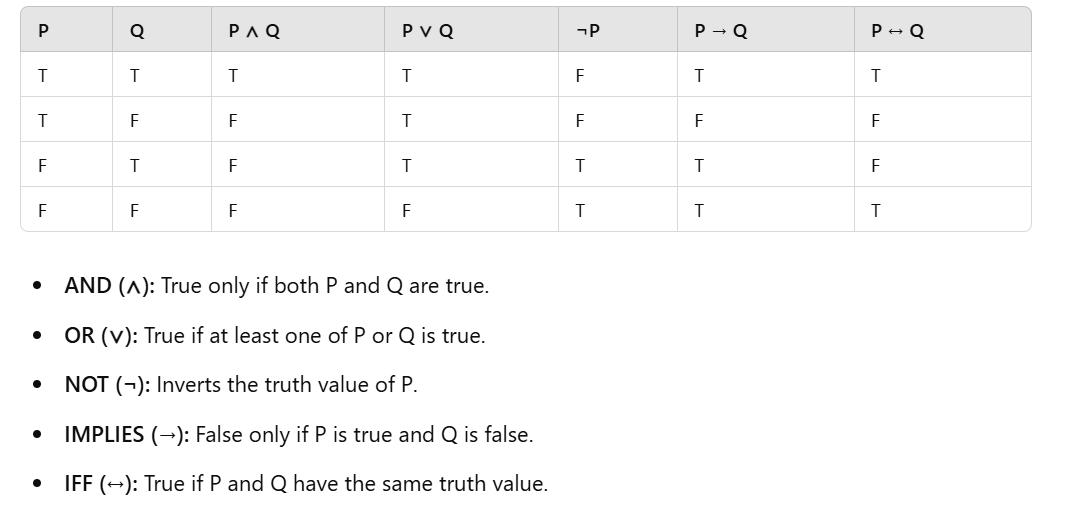
3.) Formal Logic Connectives:
Logical connectives (also known as logical operators) are symbols used to combine or modify propositions. The most common connectives in propositional logic are:

4.) Truth Tables:
A truth table is a systematic way to determine the truth value of logical expressions for all possible values of their propositions.
Truth Table for AND (∧):
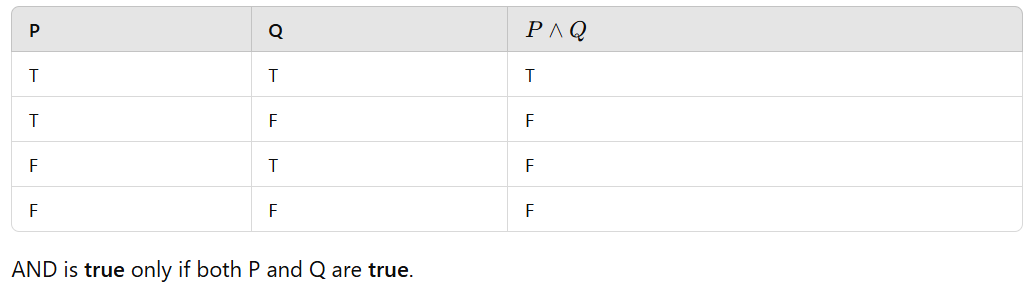
5.) Tautology:
A tautology is a logical statement that is always true, regardless of the truth values of the individual propositions.
Example of a Tautology:
- P∨¬P (Law of Excluded Middle)
Truth table:

6.) Validity:
A logical expression or argument is valid if it is true in all possible interpretations. A valid argument means that if the premises are true, the conclusion must also be true.
Example of Validity
- Premise 1: P→Q (If it rains, the ground is wet)
- Premise 2: P (It is raining)
- Conclusion: Q (The ground is wet)
Since the conclusion logically follows from the premises, the argument is valid.
7.) Well-Formed Formula (WFF):
A well-formed formula (WFF) is a syntactically correct expression in propositional logic. It follows the rules of logical syntax and is constructed properly using:
- Propositions (atomic statements)
- Logical connectives
- Parentheses (if needed for clarity)
Examples of WFFs:
- P∨Q
- ¬(P∧Q)
- (P→Q)↔R
Examples of Non-WFFs (Incorrect Syntax):
- ∧PQ (Incorrect placement of AND)
- P∨ (Missing a second proposition)
- (P→ (Unmatched parentheses)
A well-formed formula ensures that the expression is meaningful and can be evaluated logically.
8.) Inference in Propositional Logic:
Inference is the process of deriving new statements from existing ones using logical reasoning. There are three main inference techniques in propositional logic:
1.) Inference Using Resolution:
Resolution is a rule of inference used in propositional logic and predicate logic for deducing conclusions. It works by eliminating contradictions to derive new facts.
Example:
Given the two premises:
- P∨Q (Either P is true or Q is true)
- ¬P (P is false)
By applying resolution, we conclude:
- Since P is false, Q must be true.
- This leads to the new fact: Q.
2.) Forward Chaining:
Forward chaining is a reasoning method that starts with known facts and applies inference rules to derive new facts until the goal is reached.
Example: Rules:
- P→Q (If P is true, then Q is true)
- Q→R (If Q is true, then R is true)
Given that P is true, we can infer:
- Q is true (from rule 1).
- R is true (from rule 2 using the newly inferred Q).
This process moves forward from known facts to new conclusions.
3.) Backward Chaining:
Backward chaining is a reasoning method that starts with the goal (conclusion) and works backward to see if there are supporting facts or premises to prove it.
Example: Goal: Prove R is true
Rules:
- P→Q
- Q→R
To prove R, we check if Q is true (since Q→R).
To prove Q, we check if P is true (since P→Q).
If P is found to be true, then we can conclude Q is true, and finally R is true.
Backward chaining is commonly used in expert systems and AI reasoning to find solutions by tracing back from the goal.
